KVHS Northeim 2025 : Astronomie - eine Reise durch Raum und Zeit

Arithmetik - Zahlen und Mengen

Links

Wikipedia - Algebra
Wikipedia - Natürliche Zahl
Wikipedia - Ganze Zahl
Wikipedia - Rationale Zahl
Wikipedia - Reelle Zahl
Wikipedia - Komplexe Zahl
Wikipedia - Primzahl

Übersicht

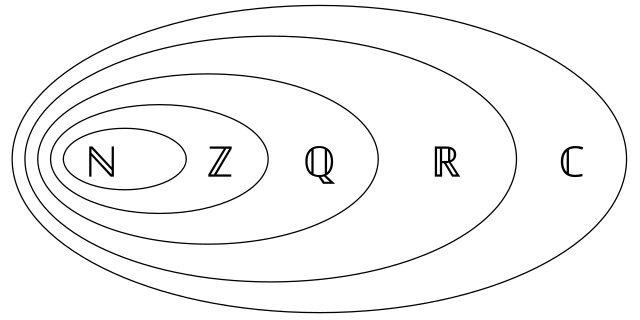
Gruppierung der unterschiedlichen Zahlenmengen:
- Natürliche($\mathbb{N}$)-, Rationale($\mathbb{Q}$)-, Ganze($\mathbb{Z}$)-, Reelle($\mathbb{R}$)- und Komplexe($\mathbb{C}$)-Zahlen
- Primzahlen, Kryptographie

Arithmetik - Natürliche Zahlen

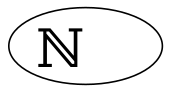
Menge der Natürlichen Zahlen $\mathbb{N}$

Definition:

alle positiven ganzen Zahlen - also zum Zählen
Symbol: $\mathbb{N}$
schon in der Steinzeit bekannt: die Zahlen von $1$ bis $10$, welche mit den Fingern darstellbar sind.
Erweiterung auf den Zahlenbereich der Natürlichen Zahlen $\boxed{\mathbb{N} \equiv \big[ 1,2,3,4,..,1000,1001,.. +\infty \big]}$
"die Zahl $z$ (Kasten mit Namen "z") beiinhaltet genau eine Zahl aus dem Bereich der Natürlichen Zahlen."
Kurzschreibweise: $z \in \mathbb{N}$
Beispiele: $\mathbb{N} = {1, 2, 3, 4, 5, ..}$
Manchmal wird auch die $0$ eingeschlossen: $\mathbb{N_0} = {0, 1, 2, 3, ..}$
Merkmale:
- Keine Kommazahlen
- Keine negativen Zahlen
- Unendlich viele

Arithmetik - Ganze Zahlen

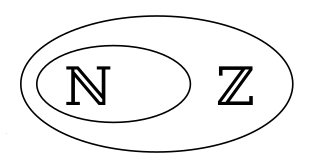
Definition: alle natürlichen Zahlen, deren negativen Gegenzahlen und die Null.
Symbol: $\mathbb{Z}$ (vom deutschen "Zahlen")
Natürliche Zahlen erweitert mit negativen natürlichen Zahlen
$\boxed{\mathbb{Z} \equiv \big( -\infty..-1000,-999,..,-1,0,1,2,..,1000,1001,.. +\infty \big)}$
Beispiele: $\mathbb{Z} = {.., -3, -2, -1, 0, 1, 2, 3, ..}$
Merkmale:
- Keine Kommazahlen
- Symmetrisch um 0

Arithmetik - Rationale Zahlen

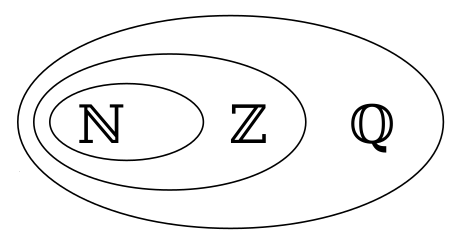
Menge der Rationalen Zahlen $\mathbb{Q}$

Definition: alle Zahlen, die als Bruch zweier ganzer Zahlen dargestellt werden können, mit Nenner ≠ 0
Symbol: $\mathbb{Q}~$ (vom lateinischen "Quotient")
Bruchzahlen, also Zahlen, welche sich aus ganzen Brüchen mit Zähler und Nenner ergeben
Ganze Zahlen erweitert mit Zahlen, welche in der Form $z = \dfrac{p}{q}$ darstellbar sind:
$\boxed{\mathbb{Q} \equiv \big( -\infty..-\dfrac{3}{2},..,-1.0,0,\dfrac{1}{2},\dfrac{8}{8},\dfrac{335}{12},..,\dfrac{999}{5},.. +\infty \big)}$
Beispiele: $\mathbb{Q} = \{1/2, -4, 7, 0.25, -1.333.., 5/8, 0\}$
Merkmale:
- Beinhaltet ganze Zahlen (z.B. $3 = 3/1$)
- Endliche oder periodische Dezimalzahlen

Arithmetik - Reelle Zahlen

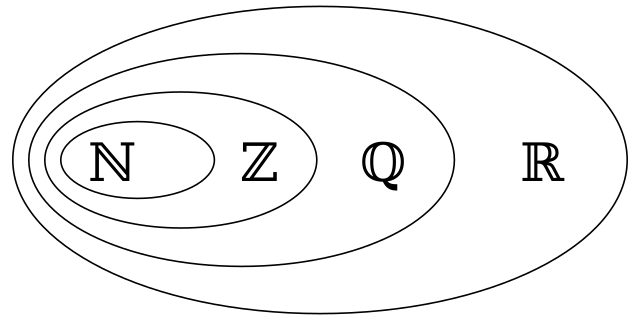
Definition: Zahlen, die nicht als Bruch dargestellt werden können. Ihre Dezimaldarstellung ist unendlich und nicht periodisch.
Symbol: $\mathbb{R}~$
Beispiele: $\sqrt{2}, ~\pi, ~e, ~\phi \text{(Goldener Schnitt)}$
Merkmale:
- Nicht darstellbar als einfache Brüche
- Unendliche, nicht wiederholende Nachkommastellen

Arithmetik - Komplexe Zahlen

Es existiert eine Komplexe Zahl $i$, welche keine Reelle Zahl ist: $\boxed{i := \sqrt{-1}=: j}$
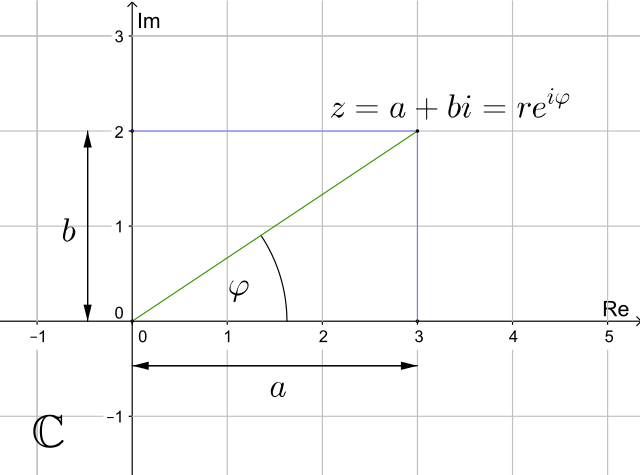
Jede Komplexe Zahl $z$ lässt sich in einen Real($R$)- und einen Imaginär($I$)-Teil aufspalten:
$z = a + j b~$ mit $~\boxed{a = R(z) = R(a + j b)}~$ und $~\boxed{b = I(z) = I(a + j b)}$
Komplexe Zahl in Exponentialform: $z = a + j b = r \exp{j \varphi}$
Umrechnung Kartesische- und Polar-Koordinaten:
$\boxed{a = r \cos(\varphi)}$ und $\boxed{b = r \sin(\varphi)}$ $\Longleftrightarrow$ $\boxed{\varphi = \arctan{\dfrac{b}{a}}}$ und $\boxed{r = \sqrt{a^2 + b^2}}$

Komplexe Zahl: Kartesische- und Polar-Koordinaten

Arithmetik - Primzahlen

- Eine Primzahl $P$ ist eine Natürliche Zahl, die genau zwei Teiler hat und somit grösser als $1$ ist.
- Beispiel: Menge aller Primzahlen $P$ im Intervall $1..100$:
$P \in \big[2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,71,73,79,83,89,97\big]$

Arithmetik - Kryptograhie

- Eindeutige Verschlüsselung und Entschlüsselung von "sicheren" Zahlen.
- Grosse Primzahlen werden in der Krytographie benötigt.