KVHS Northeim 2025 : Astronomie - eine Reise durch Raum und Zeit

Physik - Bewegungsgleichungen

Links

- Wikipedia : Galileo Galilei
- Studyflix : Weg-Zeit-Diagramm
- Studyflix : Beschleunigung

Herleitung "einfacher" Bewegungsgleichungen

Mathematische Physik:

- Grundlage: Newton2 : $\boxed{F=m \cdot a}$
- $\boxed{v = \dfrac{ds}{dt}}$ : Geschwindigkeit berechnet sich mit der ersten Ableitung des Ortes nach der Zeit.
- $\boxed{a = \dfrac{dv}{dt} = \dfrac{d^2s}{dt^2}}$ : Beschleunigung gleich erste Ableitung der Geschwindigkeit nach der Zeit
und damit Beschleunigung gleich zweite Ableitung des Ortes nach der Zeit.

Aufgaben zur Lösung einer Bewegungsgleichung
- Aufstellen der Bewegungsgleichung
- Läsen der Bewegungsgleichung

Beispiel: Freier Fall einer Masse im Schwerefeld der Erde
- Aufstellen aller Grössen und Anfangsbedingungen:
$g = 9.81 \dfrac{m}{s^2}$ : Erdbeschleunigung (Bekannt)
$s(t_0) = s_0$ : Anfangsort (bekannt)
$v(t_0) = v_0$ : Anfangsgeschwindigkeit (bekannt)
- Aufstellen der Bewegungsgleichung:
$\boxed{m \cdot a = \dfrac{d^2 s(t)}{dt^2}= m \cdot g}$
- Lösen der Bewegungsgleichung durch doppelte Integration:
$\boxed{s(t) = s_0 + v_0 t + \dfrac{g}{2}t^2}$
- Bewegung damit vollständig berechenbar und bestimmt!

Beispiel: Gleichförmige unbeschleunigte Bewegung

Annahme: Newton1 : $\boxed{a = 0 \Rightarrow F=m \cdot a = 0}$
Folgerung:
$a = 0 = \dfrac{dv}{dt} = \dfrac{d^2s}{dt^2}$
$\int\limits_0^t{0}dt = \int\limits_0^t{\dfrac{d^2s}{dt^2}dt}$
$0 = v(t) - v_0$
$v_0$ : bekannte Anfangsgeschwindigkeit in $[v_0] = \dfrac{m}{s}$
Beschleunigung null ⇒ Geschwindigkeit bleibt konstant :
$\boxed{a = 0}$ $\Rightarrow$ $\boxed{v(t) = v_0}$

$\int\limits_0^t{\dfrac{ds(t)}{dt}dt} = \int\limits_0^t{v_0 dt}$
$\int\limits_0^s{ds} = v_0 \int\limits_0^t{dt}$
$s(t) - s(t_0) = v_0 (t - t_0)$
$s_0$ : bekannter Anfangsort in $[s_0] = m$
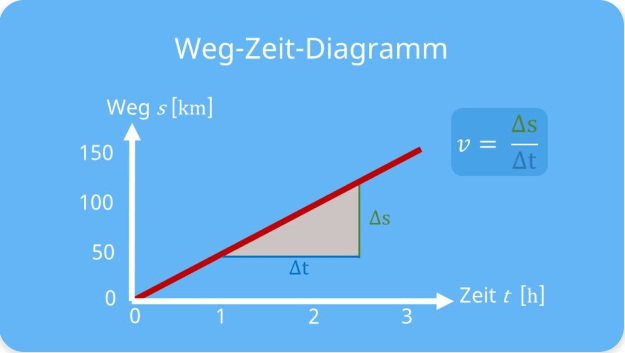
Beschleunigung null ⇒ Weg wächst linear mit der Zeit :
$\boxed{a = 0}$ $\Rightarrow$ $\boxed{s(t) = s_0 + v_0 t}$
Ergebnis:
- Erfährt ein Körper keine Beschleunigung ($a=0$), so verbleibt er in Ruhe bzw. bewegt
sich gradlinig mit konstanter (Anfangs-)Richtung und (Anfangs-)Geschwindigkeit $v_0$.

Beschleunigung:null : lineares Weg-Zeit-Diagramm

Beschleunigung:null : Geschwindigkeit(const)-Zeit-Diagramm

Beispiel: Gleichförmig beschleunigte Bewegung

Annahme: Newton1 : $\boxed{a, m = const \Rightarrow F = const}$
Folgerung:
$a = a_0 \Rightarrow a_0 = \dfrac{d^2s}{dt^2} = \dfrac{dv}{dt} \Rightarrow a_0 = \dfrac{dv}{dt}$
$\int\limits_0^t{a_0 dt} = a_0 \int\limits_0^t{ dt} =\int\limits_0^tdv$
$a_0 t = v(t) - v_0$
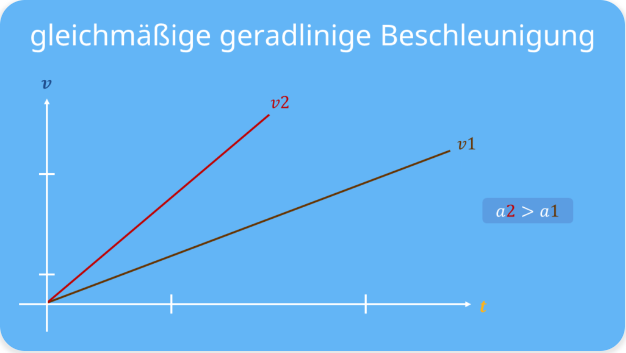
Beschleunigung konstant ⇒ Geschwindigkeit wächst linear mit der Zeit :
$\boxed{a = a_0 = const}$ $\Rightarrow$ $\boxed{v(t) = v_0 + a_0 t}$

$\int\limits_0^t{\dfrac{ds}{dt}dt} = \int\limits_0^t{(v_0 + a_0 t)dt}$
$\int\limits_0^s{ds} = \int\limits_0^t{v_0 dt} + \int\limits_0^t{a_0 t dt}$
$s(t) - s_0 = v_0 t + a_0 \dfrac{t^2}{2}$
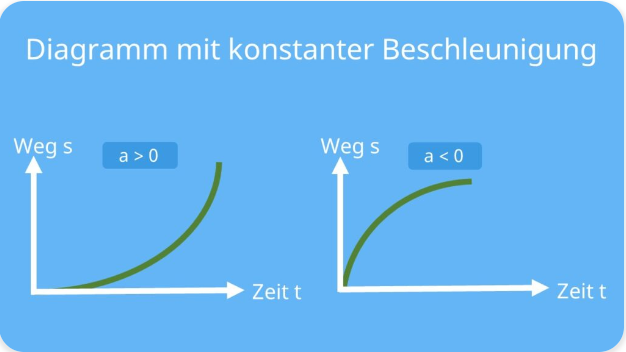
Beschleunigung konstant ⇒ Weg wächst quadratisch mit der Zeit :
$\boxed{a = a_0 = const}$ $\Rightarrow$ $\boxed{s(t) = s_0 + v_0 t + \dfrac{a_0}{2}t^2}$

Beschleunigung:const : quadratisches Weg-Zeit-Diagramm

Beschleunigung:const : lineares Geschwindigkeit-Zeit-Diagramm

Beispiel:
Im Schwerefeld der Erde wirkt ein konstante Erdbeschleunigung mit
$g=9.81\dfrac{m}{s^2}$ auf eine Probemasse $m$ :

Experiment:
- Messtabelle von Weg $s$ : $[s]=m$ und Zeit $t$ : $[t]=s$
- Abhängigkeit : $\boxed{s \propto t^2}$ : Weg proportional dem Quadrat der Zeit
- Beschleunigung entspricht Erdbeschleunigung: $\boxed{a = g = 9.81 \dfrac{m}{s^2}}$
Ergebnis:
- Gesetz : $\boxed{s(t) = \dfrac{g}{2} t^2}$ (eigentlich $\boxed{s(t) = s_0 + v_0 t + \dfrac{g}{2}t^2}$) wird mit Messung best&?uml;tigt!
- damit wächst beim freien Fall der zurückgelegte Weg $s$ quadratisch mit der Zeit $t$!
- Weg- und Geschwindigkeitsgesetz sind unabhängig von der Masse!

Beispiel: Experimentelle Herleitung des Freien-Fall-Gesetzes

- Erste Versuche dieser Art von Galileo Galilei (1590)
- Messung von Weg $s$ : $[s]=m$ und Zeit $t$ : $[t]=s$
- Abhängigkeit : $s \propto t^2$
- Gesetz : $\boxed{s = \dfrac{g}{2} t^2}$ (122) mit Erdbeschleunigung $g=9.81 \dfrac{m}{s^2}$
damit wächst beim freien Fall der zurückgelegte Weg $s$ quadratisch mit der Zeit $t$!

Beispiel: Theoretische Herleitung des Erdbeschleunigung

- Probemasse $m$ wird von der Erdenmasse $M=5.972 \cdot 10^{24}kg$ angezogen
- Abstand $m$ vom Erdmittelpunkt sind $R = 6371.2km = 6371200m$
- $G=6.6743 \cdot 10^{-11} \dfrac{m^3}{kg \cdot s^2}$ : Gravitationskonstante
- Masse $m$ erfährt eine Beschleunigung: $F_m = m \cdot a$
- Zwischen Probemasse und erde gilt das Gravitationsgesetz $F_m = G \cdot \dfrac{m \cdot M}{r^2}$
- mit $R = r$ : $F_m = G \cdot \dfrac{m \cdot M}{R^2}$
- Gleichsetzen: $F_m = m \cdot a = F_m = G \cdot \dfrac{m \cdot M}{R^2}$
    $ma = G \cdot \dfrac{m \cdot M}{R^2}$ $~~\Rightarrow~~ a = G \cdot \dfrac{M}{R^2} =: g$
    Die Beschleunigung $a$ der Masse $m$ zum Erdmittelpunkt ist NICHT von der Masse sondern
    nur von der Masse der Erde $M$, dem Erdradius $R$ und der Gravitationskonstanten $G$ abhängig!

- die Erdbeschleunigung berechnet sich mit $\boxed{g = G \cdot \dfrac{M}{R^2}}$ (123) :

$g = 6.6743 \cdot 10^{-11} \dfrac{m^3}{kg \cdot s^2} \cdot \dfrac{5.972 \cdot 10^{24}kg}{6371200^2 \cdot m^2} = 9.81 \cdot 10^{-13}\cdot 10^{-11} 10^{24}\dfrac{m^3}{kg \cdot s^2} \cdot \dfrac{kg}{ m^2}$
$g = 9.81 \dfrac{m^3 \cdot kg}{kg \cdot s^2 \cdot m^2} ~~\Rightarrow ~~ \boxed{g = 9.81 \dfrac{m}{s^2}}$ (124)

Damit wurde die Vorgabe oben theoretisch korrekt berechnet!