| WebSites | Inhalt | Unser Sonnensystem | Unser Wissen |
KVHS Northeim 2025 : Astronomie - eine Reise durch Raum und Zeit
Eratosthenes : Berechnung des Umfangs der Erde
Links
- Planet Wissen : Eratosthenes und der Erdumfang
Problem
Im 4. Jahrhundert vor Christus behauptete der Philosoph Aristoteles:
Die Erde ist keine Scheibe, sondern eine Kugel.
150 Jahre später berechnete der Grieche Eratosthenes mit einfachen Mitteln dann erstaunlich genau den Erdumfang zu $40000 km$.
Überlegung
Gegeben:
- - Sonne scheint mit parallelen Strahlen auf die Erde (unendlich weit entfernt).
Die Erde sei eine Kugel mit Radius $R$ und Umfang $U$.
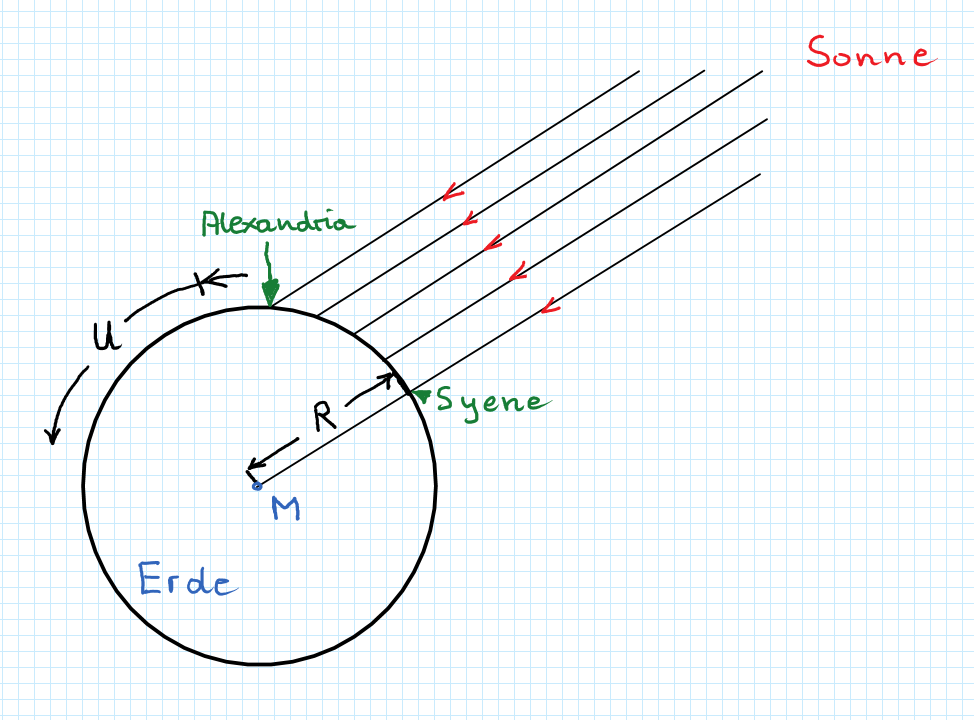
Geometrie Problem Erdradius
- - Zur Mittagszeit (Frühlingsanfang) steht die Sonne senkrecht über dem Brunnen in Syene,
Deutlich sieht man in der Mitte der Wasseroberfläche des Brunnens das Spiegelbild der Sonne.
Daher bildet die senkrechte Sonne keinen Schatten.
Zur gleichen Zeit misst ein Beobacher in Alexandria sehr wohl neben einem Turm bekannter Höhe $H$ einen Schatten der Länge $S$
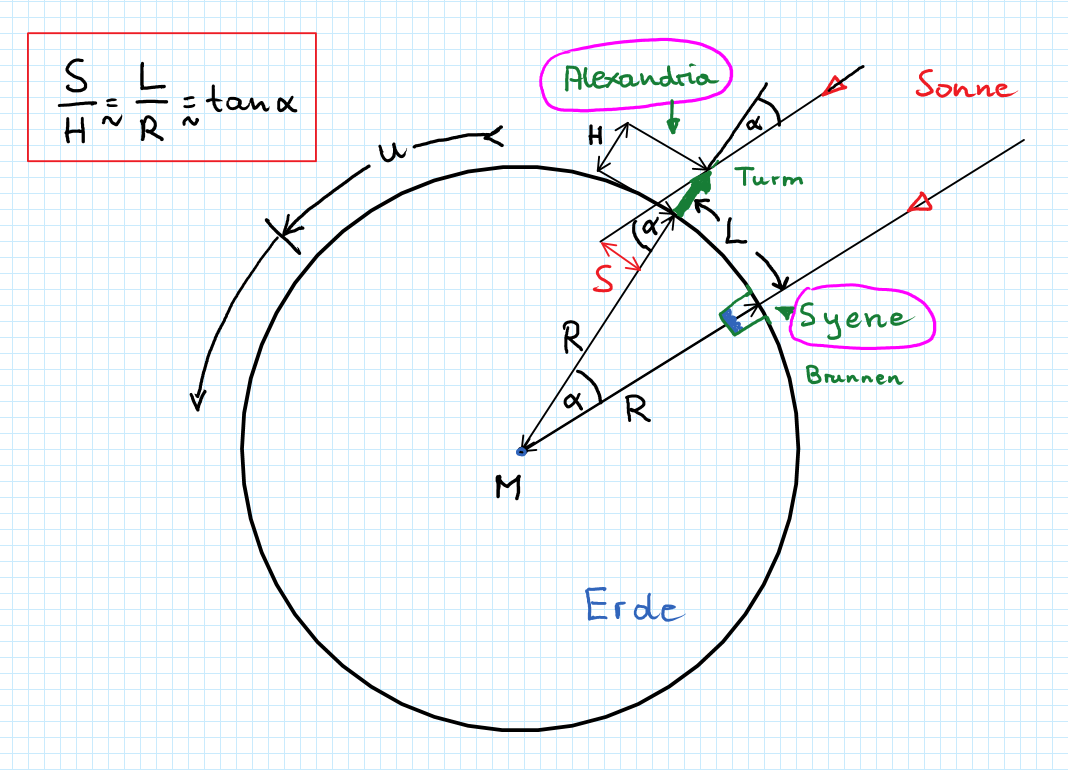
Geometrie detailliert zur Berechnung des Erdradius
- - $R = ?$ : unbekannter Radius der Erde
- - $S = 1.23m$ : Schattenlänge neben dem Turm in Alexandria
- - $H = 10m$ : Höhe des dem Turms in Alexandria
- - $L = 5000 \cdot 157.5m$ : Entfernung zwische Alexandria und Syene (5000 Ellen)
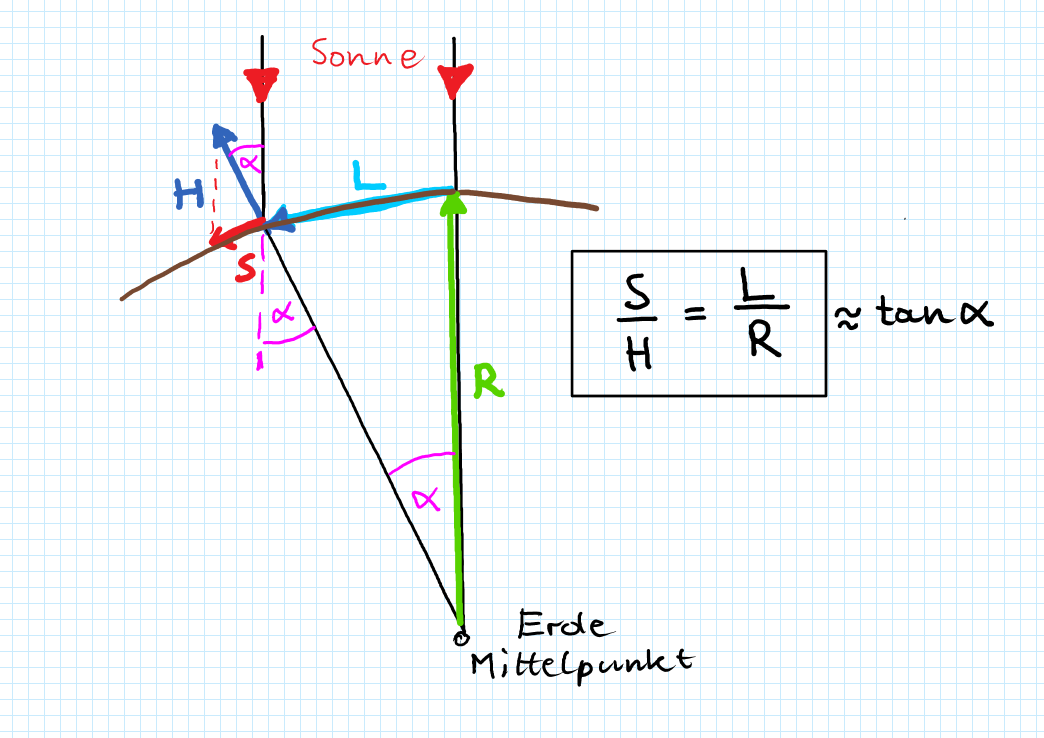
Geometrie detailliert zur Berechnung des Erdradius
Gesucht:
- - $R = ?$ : unbekannter Radius der Erde
- - $U = ?$ : Umfang der Erde
Lösung
Radius der Erde
Die beiden Dreieckte $S-Alexandia-H$ und $M-Syene-A$ besitzen den gleichen Stufenwinkel $\alpha$.
$\Rightarrow~~ \boxed{\dfrac{S}{H} = \dfrac{L}{R}} = \tan{\alpha}$ (1)
Auflösung nach dem unbekannten Erdradius $R$ :
$\dfrac{S}{H} = \dfrac{L}{R} ~~\vert~~ Kehrwert$
$\dfrac{H}{S} = \dfrac{R}{L} ~~\vert~~ \cdot L$
$\boxed{R = \dfrac{H \cdot L}{S}}$ (2)
Einsetzen:
$R = \dfrac{10m \cdot 5000 \cdot 157.5m}{1.23m}$
$R = \dfrac{10 \cdot 5000 \cdot 157.5 m^2}{1.23m}$
$R = \dfrac{7875000 m}{1.23}$
$\boxed{R = 6402000m = 6402km}$ (3)
Google: Radius der Erde: $\boxed{R_{Google} = 6378km}$ (4)
Umfang der Erde
$\boxed{U = 2 \cdot \pi \cdot R}$ (5)
Einsetzen:
$U = 2 \cdot \pi \cdot 6402km$
$\Rightarrow \boxed{U = 40225 km}$ (6)
Ergebnis
Die Erde sei eine Kugel mit Radius $R$ und Umfang $U$.

Deutlich sieht man in der Mitte der Wasseroberfläche des Brunnens das Spiegelbild der Sonne.
Daher bildet die senkrechte Sonne keinen Schatten.
Zur gleichen Zeit misst ein Beobacher in Alexandria sehr wohl neben einem Turm bekannter Höhe $H$ einen Schatten der Länge $S$


Damit hat Eratosthenes im 2ten Jahrhundert BC
- - die Kugelgestalt der Erde richtig erkannt,
- - den Erdradius auf ein halbes Prozent genau auf $\boxed{R = 6402km}$ bestimmt!
- - den Umfang der (kreisförmigen) Erde auf $\boxed{U = 40225 km}$ berechnet!
| WebSites | Inhalt | Unser Sonnensystem | Unser Wissen |