KVHS Northeim 2025 : Astronomie - eine Reise durch Raum und Zeit

Helligkeit und Entfernung von Sternen

Links

- Wikipedia : Scheinbare Helligkeit von Sternen
- Wikipedia : Absolute Helligkeit von Sternen
- LEIFIphysik : Entfernungsbestimmung mit Cepheiden
- Wikipedia : Cepheiden
- Wikipedia : Offener Sternhaufen NGC7790

Überblick

Wenn wir den Nachthimmel betrachten, sehen wir leuchtende Sterne. Dabei empfinden wir mit blossem Auge, dass die Sterne unterschiedlich hell leuchten. Die Helligkeit, mit der wir einen Stern auf der Erde mit blossem Auge wahrnehmen, wird als scheinbare Helligkeit eines Sternes bezeichnet.

Da die Helligkeit der Sterne aber nicht nur von ihrer Grösse abhängt, sondern auch von der Entfernung zum Betrachter, hat man die absolute Helligkeit von Sternen eingeführt, damit diese vergleichbar sind.

Kurz zusammengefasst lässt sich sagen: Die scheinbare Helligkeit eines Sternes sagt aus, wie hell ein Stern uns am Erd-Himmel erscheint, während die absolute Helligkeit die wirkliche Strahlungsleistung eines Sterns wiedergibt.

Absolute und scheinbare Helligkeit bei Sternen
Wie eingangs erwähnt, hängt die Helligkeit eines Sternes (den wir am Himmel sehen) nicht nur davon ab, wie stark der Stern leuchtet (also wie gross der Stern ist => siehe Kapitel Hertzberg-Russel-Diagramm), sondern auch von der Entfernung des Sternes zu uns. Daher erscheint uns die Sonne im Vergleich zu anderen Sonnen als ein sehr heller Stern, obwohl andere Sterne heller leuchten (absolut gesehen), aber sehr weit entfernt ist.

Betrachten wir also einen Stern am Erdhimmel, nehmen wir die scheinbare Helligkeit eines Sterns wahr. Die scheinbare Helligkeit ist die Helligkeit von Sternen, so wie wir sie auf der Erde sehen. Die scheinbare Helligkeit wird heutzutage immer noch verwendet, da (immer noch) nach dieser “Grösse” Sterne in unterschiedliche Grössenklassen eingeteilt werden (der griechische Astronom Hipparchos klassifizierte ca. 120 v. Chr. die Sterne nach dieser Methode).

Seitdem sind Sterne, die mit blossem Auge auf der Erde sichtbar sind, in sechs Grössenklassen (den sogenannten Magnituden) eingeteilt. Dabei erhalten die hellsten Sterne den Wert $1 mag$ und werden als die erste Grössenklasse bezeichnet. Die von der Erde aus gerade noch sichtbaren Sterne erhalten den Wert $6 mag$ und stellen die sechste Grössenklasse dar. Die scheinbare Helligkeit wird mit dem Symbol $m$ angegeben und trägt die Einheit [m]=mag$. Bei der scheinbaren Helligkeit gilt: Je kleiner der Wert, desto heller erscheint uns der Stern.

Mit Hilfe geeigneter Kameras (CCD-Kameras) und einigen Physikkenntnissen (oder einer geeigneten Software) kann die scheinbare Helligkeit eines Sternes bestimmt werden (man benötigt hierfür die Entfernung zum Stern und die Intensität der vom Messgerät gemessenen elektromagnetischen Strahlung, die vom Stern emittiert wurde und den Beobachter auf der Erde erreicht).

Wie aber schon eingangs erwähnt, ist die scheinbare Helligkeit keine Grösse, die wirkliche Leuchtkraft oder absolute Helligkeit eines Sterns angibt bzw. mit der man Sterne vergleichen kann. Damit man aber nun die Helligkeit verschiedener Sterne miteinander vergleichen kann, hat man in der Astronomie die absolute Helligkeit eingeführt. Die absolute Helligkeit ist die Helligkeit, die ein Stern in einem Abstand von zehn Parsec hätte (dies gilt für alle Sterne). Die absolute Helligkeit sagt also aus, wie hell uns ein Stern auf der Erde erscheinen würde, wenn er sich von uns 10 Parsec identisch 32.616 Lichtjahren entfernt befände. Dies ermöglicht somit Vergleich zwischen den Sternen.

Berechnung Absolute Helligkeit aus Entfernung und Scheinbarer Helligkeit

Für die absolute Helligkeit können wir auch eine Formel angeben, da sie nichts anders ist, als die scheinbare Helligkeit, wenn sich der Stern von uns im Abstand von 10 Parsec befände.

R in Parsec:
$\boxed{M = m - 5mag \cdot \log_{10}(\dfrac{R[pc]}{10pc})}$ (1.1)
R in Lichtjahren:
$\boxed{M = m - 5mag \cdot \log_{10}(\dfrac{R[ly]}{32.616ly})}$ (1.2)
R in Astronomischen Einheiten:
$\boxed{M = m - 5mag \cdot \log_{10}(\dfrac{R[au]}{2062650au})}$ (1.3)
R in Kilometern:
$\boxed{M = m - 5mag \cdot \log_{10}(\dfrac{R[km]}{3.08568 \cdot 10^{14} km})}$ (1.4)

$M$ : absolute Helligkeit eines Sterns, $[M]=mag$
$m$ : scheinbare Helligkeit eines Sterns, $[m]=mag$
$R$ : Abstand zur Erde, $[R]= pc|ly|au|km$

Beispiel Sonne:
Wir bestimmen eine scheinbare Helligkeit der Sonne mit einem Intensitätsmessgerät auf der Erde mittags zu $m = -26.8mag$.
Die (mittlere astronomische) Entfernung Sonne Erde ist $R = 1.496 \cdot 10^8 km$ ($1 AE$ Astronomischen Einheit).
Eingesetzt in Gleichung (1.3) ergibt für die absolute Helligkeit der Sonne von $M$ :

$M = m - 5mag \cdot \log(\dfrac{R}{3.08568 \cdot 10^{14} km})$
$M = -26.8 mag - 5mag \cdot \log_{10}(\dfrac{1.496 \cdot 10^8 km}{3.08568 \cdot 10^{14} km})$
$M = -26.8 mag - 5mag \cdot \log_{10}(0.485 \cdot 10^{-6})$
$M = -26.8 mag - 5mag \cdot \big[\log_{10}(0.485) + \log_{10}(10^{-6})\big]$
$M = -26.8 mag - 5mag \cdot \big[-0.3148 - 6\big]$
$M = -26.8 mag - 5mag \cdot \big[-6.3148\big]$
$M = -26.8 mag + 31.574mag$
$\boxed{M = 4.8 mag}$ (1.5)

Das Entfernungsmodul

definiert als: $\boxed{m - M := 5 mag \cdot \log_{10}(\dfrac{R[pc]}{10pc}) }$ (2.1)
steht damit in einem festen Zusammanhang mit der Entfernung:
$\boxed{R = 10pc \cdot 10^{\dfrac{m - M}{5 mag}}}$ (2.2)

Die Perioden-Helligkeits-Relation von Cepheiden:

$\boxed{M = a \cdot \log_{10}\big(\dfrac{T}{1d}\big) +b}$ (2.3) Henriette-Leavitt-Gesetz
zu fittende Parameter aus physikalischen NukleoSynthese-Kenntnissen bekannter Cepheiden:
$a$, $[a]=mag$
$b$, $[b]=mag$

Beispiel Cepheiden

Ist die Absolute Helligkeit $M$ eines Cepheiden über die Helligkeits-Schwankungs-Periode bekannt:
$M = M(T_{pulse})$ , so kann über die Scheinbare Helligkeit $m$ (gemessen auf der Erde) die Entfernung des Cepheiden nebst seiner Umgebung (Galaxy) berechnet werden!

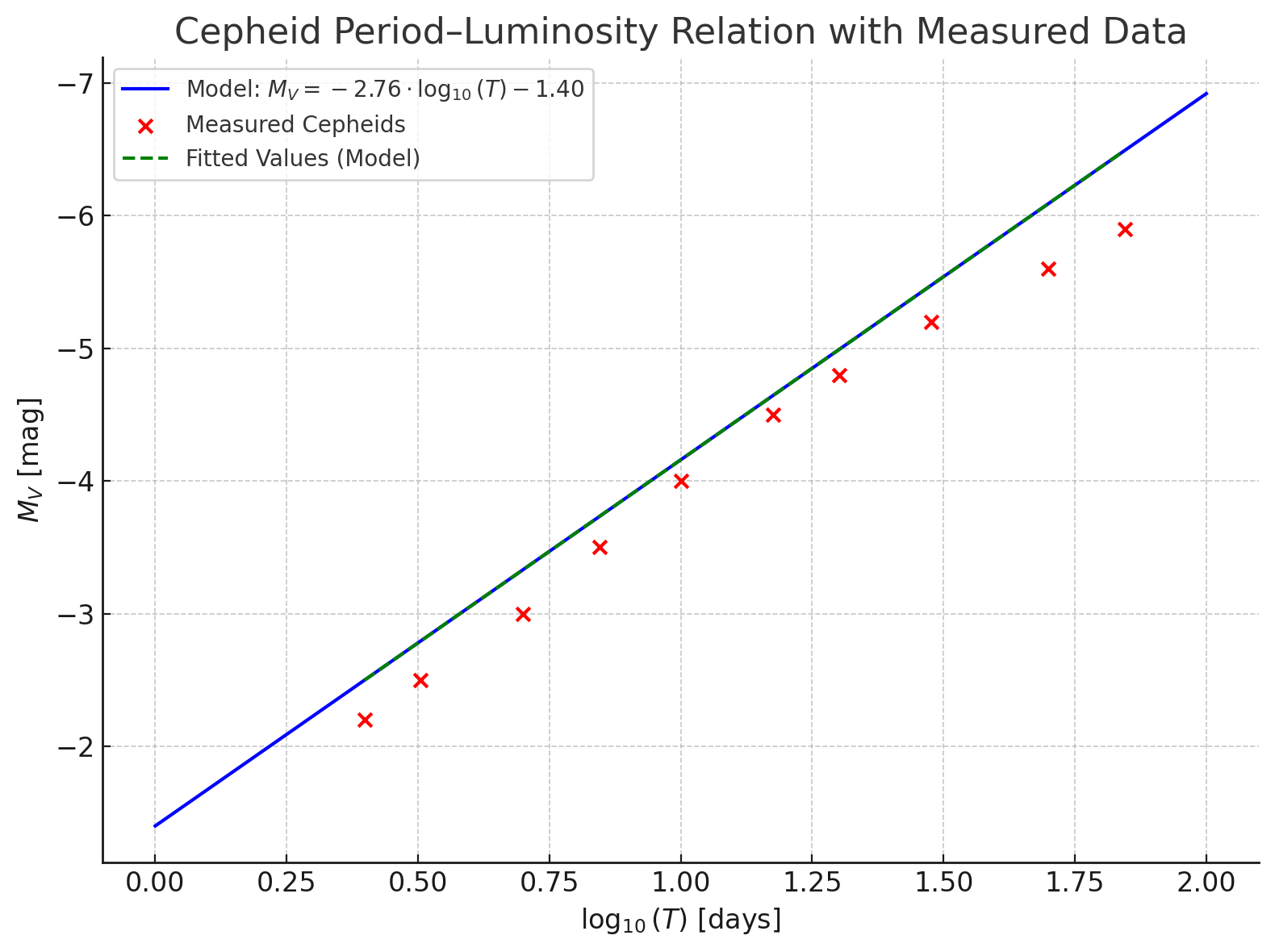
Typische Cepheiden-Relation in unserer Milchstrasse und damit im gesamten Universum:
$\boxed{M = -2.76mag \cdot \log_{10}\big(\dfrac{T}{1d}\big) - 1.4mag}$ (2.4)

Beispiel: Entfernung zum Offenen Sternhaufen NGC7790 (Cassiopeia)

NGC 7790 ist ein offener Sternhaufen im Sternbild Cassiopeia und enthält drei bekannte Cepheiden:

CEa Cassiopeiae (CEa Cas) :
Periode $\boxed{T_{CEa}=5.6d}$ , Scheinbare Helligkeit $\boxed{m = 11.5 mag}$
CEb Cassiopeiae (CEb Cas) :
Periode $T_{CEb}=4.88d$
CF Cassiopeiae (CF Cas) :
Periode $T_{CF}=4.88d$

mit $\boxed{P_{CEa}=5.6d}$ ergibt sich die Absolute Helligkeit des Sterns CEa Cassiopeiae :
$\boxed{M = -2.76mag \cdot \log_{10}\big(\dfrac{T_{CEa}}{1d}\big) - 1.4mag}$ (*2.4)
Gegeben: $\boxed{T_{CEa}=5.6d}$ $~\Rightarrow~$ $\boxed{M = -3.47 mag}$

Berechnung der Entfernung:
$\boxed{R = 10pc \cdot 10^{\dfrac{m - M}{5 mag}}}$ (*2.2)
mit $\boxed{m = 11.5 mag}$ und $\boxed{M = -3.47 mag}$ $~\Rightarrow~$ $\boxed{\boxed{R_{NGC7790}=98700pc}}$ ???
Dieses Ergebnis ist deutlich grösser als der heute bekannten Wert für den Sternhaufen NGC 7790
Google: $R_{Google NGC7790}=2944pc$ (ca. 3.5–4 kpc)
Das liegt daran, dass wir in dieser Beispielrechnung:

keine Korrektur für Extinktion (interstellare Abschwächung) vorgenommen haben,
eine vereinfachte Leuchtkraftbeziehung verwendet haben,
nicht-kalibrierte Werte für $m$ nutzen.

Fragen und Antworten: Absolute und Scheinbare Helligkeit von Sternen

1. Was ist die absolute Helligkeit eines Sterns?
Die absolute Helligkeit ist ein Mass dafür, wie hell ein Stern von einer festgelegten Entfernung aus, in der Regel von 32,6 Lichtjahren oder 10 Parsec, erscheinen würde.

2. Was ist die scheinbare Helligkeit eines Sterns?
Die scheinbare Helligkeit ist ein Mass dafür, wie hell ein Stern von der Erde aus erscheint. Sie hängt sowohl von der absoluten Helligkeit des Sterns als auch von seiner Entfernung zur Erde ab.

3. Wie stehen absolute und scheinbare Helligkeit miteinander in Verbindung?
Im Allgemeinen gilt: Je grösser die Entfernung eines Sterns von der Erde, desto kleiner ist seine scheinbare Helligkeit, unabhängig von seiner absoluten Helligkeit.

4. Welche Masseinheit wird üblicherweise für die Helligkeit von Sternen verwendet?
Diese wird in den meisten Fällen in der Einheit Magnitude angegeben.

5. Wie ändert sich die scheinbare Helligkeit eines Sterns, wenn die Entfernung dazu verdoppelt wird?
Wenn sich die Entfernung zu einem Stern verdoppelt, nimmt seine scheinbare Helligkeit um das Vierfache ab.

6. Ist ein Stern mit einer kleineren Magnitude heller oder dunkler als einer mit einer grösseren Magnitude?
Ein Stern mit einer kleineren Magnitude ist heller als ein Stern mit einer grösseren Magnitude.

7. Wie können Astronomen die Entfernung zu weit entfernten Sternen messen?
Astronomen verwenden verschiedene Methoden, darunter die Parallaxenmethode und die Bestimmung der absoluten und scheinbaren Helligkeit eines Sterns.

8. Was ist die Parallaxenmethode?
Die Parallaxenmethode ist eine Methode zur Bestimmung der Entfernung zu Sternen. Sie basiert auf der Veränderung des scheinbaren Positionswechsels eines Sterns, wenn man ihn von zwei verschiedenen Punkten aus betrachtet.

9. Warum ist das Wissen über die absolute und scheinbare Helligkeit wichtig für die Astronomie?
Die Verbindung von absoluter und scheinbarer Helligkeit liefert wichtige Informationen über die Entfernung, Grösse, Masse und Lebensdauer eines Sterns. Jede dieser Eigenschaften kann helfen, unser Verständnis des Universums zu verbessern.