Fallgesetze - Freier Fall

Übersicht

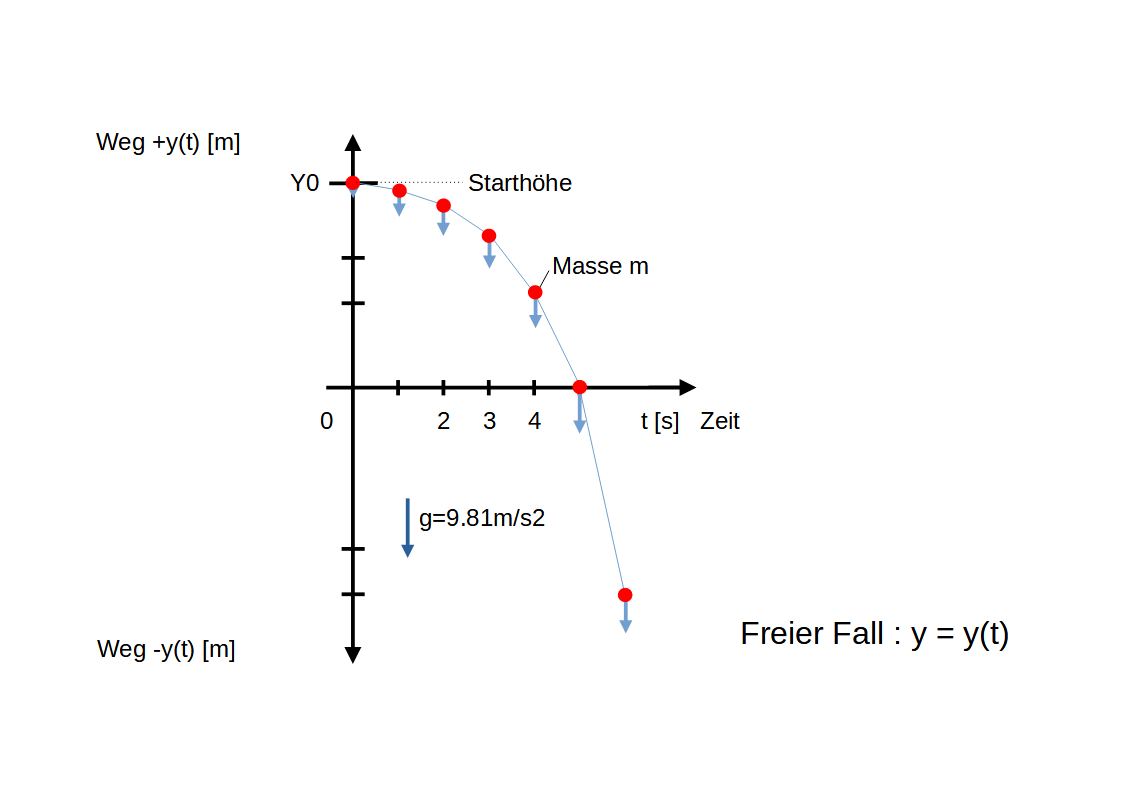
  •  Masse $m$ fällt im Schwerefeld der Erde mit der Erdbeschleunigung $g$ in negativer $y$-Richtung
  •  Bewegung in nur einer Dimension $y = y(t)$:
  •  Masse $m$ und Erdbeschleunigung $g$ werden als konstant angenommen
  •  Frei wählbarer Anfangsort $y_0$ (Fallhöhe)
  •  Anfangsgeschwindigkeit $v_0 = 0 \dfrac{m}{s}$ da freier Fall

Weg-Zeit-Funktion des Freien Falls:
$\boxed{y(t) = -\dfrac{gt^2}{2} + y_0}$ (5)
Der Weg wächst bei konstanter Beschleunigung quadratisch mit der Zeit.

Geschwindigkeit-Zeit--Funktion des Freien Falls:
$\boxed{v(t) = -gt}$ (4)
Die Geschwindigkeit wächst bei konstanter Beschleunigung linear mit der Zeit.

Fallhöhe $yh$ :
$\boxed{y_h = y_0}$ (6)

Fallzeit $t_f$ :
$\boxed{t_f = \sqrt{\dfrac{2 y_0}{g}}}$ (7)

Aufprallgeschwindigkeit $v_p$ :
$\boxed{v_p = \sqrt{2 g y_0}}$ (8)

Download

  •  Download dieser Seite als Pdf-Dokument: FreierFall.pdf

  •  Download des Python-Programms: FreierFall.py

Herleitung

Newton: $\boxed{F = - m g}$ (1)
gesucht: Umwandlung von Beschleunigung in Weg und Geschwindigkeit

Erste Integration nach der Zeit ergibt die Geschwindigkeit $v(t)$:
$\boxed{v(t) = -\int\limits_t{gdt}}$ (2)

Zweite Integration nach der Zeit ergibt den Ort $y(t)$:
$\boxed{y(t) = \int\limits_t{v(t)dt}}$ (3)

Damit folgt:
(2) : $v(t) = -\int\limits_t{gdt}$
(Geschwindigkeit zeigt in negative Y-Richtung)

$v(t) = -gt + v_0$

Freier Fall: Anfangsgeschwindigkeit $v_0 = 0 \dfrac{m}{s}$
$\boxed{v(t) = -gt}$ (4)

(3) : $y(t) = \int\limits_t{v(t)dt}$
$y(t) = \int\limits_t{[-gt + v_0]dt}$
$y(t) = -\dfrac{gt^2}{2} + v_0 t + y_0$

$v_0 = 0 \dfrac{m}{s}$

$\boxed{y(t) = -\dfrac{gt^2}{2} + y_0}$ (5)

Weitere Berechnungen

Fallhöhe

Bedingung: (5) mit $t = 0$ :
$y_h(t = 0) = -\dfrac{gt^2}{2} + v_0 t + y_0$
$\boxed{y_h = y_0}$ (6)

Fallzeit

Bedingung: (5) identisch Null:
$y(t_f) = 0 = -\dfrac{gt_f^2}{2} + y_0$
$0 = -g t_f^2 + 2 y_0$
$t_f^2 = \dfrac{2 y_0}{g}$
$\boxed{t_f = \sqrt{\dfrac{2 y_0}{g}}}$ (7)

Aufprallgeschwindigkeit

Bedingung aus (4): $v_p(t_f) := \big\vert -gt_f \big\vert$
$v_p = g\sqrt{\dfrac{2 y_0}{g}}$
$\boxed{v_p = \sqrt{2 g y_0}}$ (8)

Darstellung der Gleichungen mit Python

Sehen wir uns nun all diese Gleichungen in einem darstellenden Python Programm an: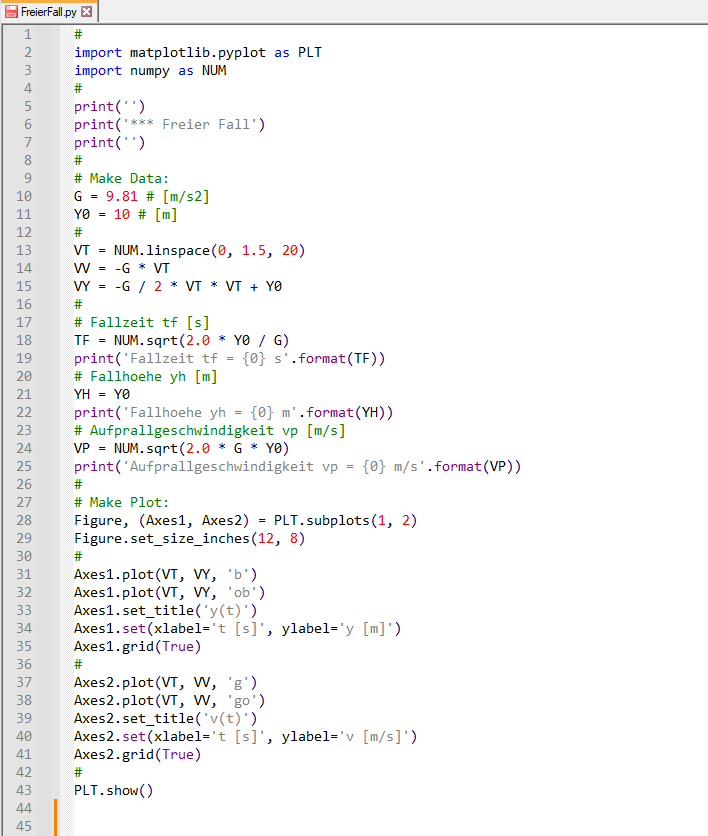


Download des Python-Programms: FreierFall.py


Das Python-Programm FreierFall startet mit der Einbindung zweier Bibliotheken:
einer Plot-Bibliothek mit Namen PLT und einer Numerischen Bibliothek mit Namen NUM.

Danach erfolgt die Ausgabe des Programm-Headers "Freier Fall".

Im folgenden Abschnitt "Make Data" werden alle Daten definiert und erzeugt.
  •  die Erdbeschleunigung G mit $9.81 \dfrac{m}{s^2}$
  •  und die Anfangshöhe Y0 mit $10m$.

Es folgt die Erzeugung eines Vektors VT über die Zeit von $0s$ bis $1.5s$ in $20$ Schritten.
Mit diesem Zeitvektor berechnet sich ein Geschwindigkeitsvektor VV und ein Ortsvektor VY.

Danach finden wir die Gleichungen für die Fallzeit TF, die Fallhöhe YH und
die Aufprallgeschwindigkeit VP.

Mit diesen Daten werden im nächsten Abschnitt "Make Plot" ein Orts-Zeit-Plot $y(t)$ gegen $t$
und ein Geschwindigkeits-Zeit-Plot $v(t)$ gegen $t$ berechnet und ausgegeben.

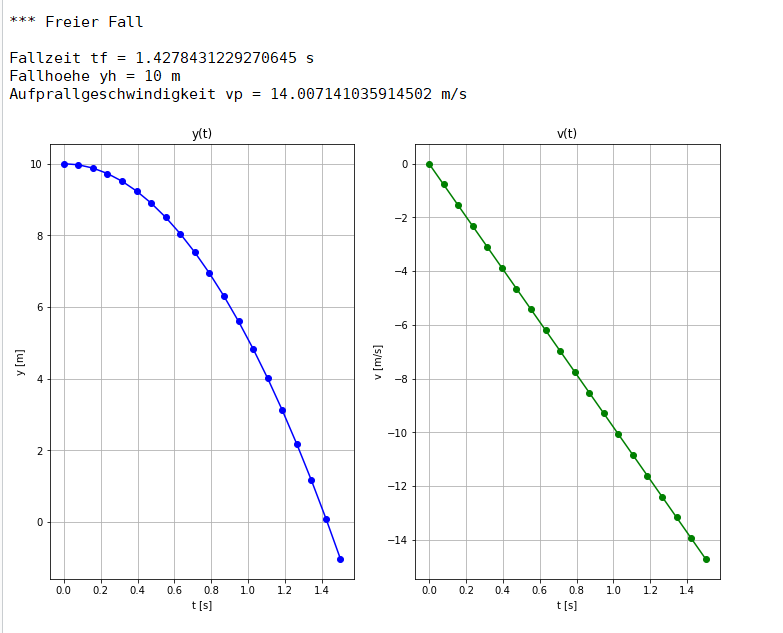
"Run" zeigt das Ergebnis der berechneten Freier-Fall-Parameter und die beiden Plots $y(t)$ und $v(t)$.

Die berechnete Fallzeit von $t_f=1.4s$ stimmt mit der Zeit für die Bewegung von $y(t=0)=yh$
bis $y(tf)=0$ überein.
Ebenso zeigt der $v(t)$ Plot die Aufprallgeschwindigkeit $v_p$ von $-14 \dfrac{m}{s}$ nach $t_f=1.4s$.


Ausgabe nach dem Start des Python-Programms:

---

WebSites    Module