Kapitel 1 : Terme und Formeln
1.0 Überblick
1.1 Terme mit mehreren Variablen
1.2 Ausmultiplizieren und Ausklammern
1.3 Binomische Formeln
1.4 Umstellen von Formeln und Gleichungen
1.5 Aussagen und Beweise
Quellen
Lambacher Schweizer: "Mathematik für Gymnasien Klasse 8" [ISBN:978-3-12-734281-9]Klett Verlag : Lambacher Schweizer Mathematik 8
GeoGebra : GeoGebra - Rechner Suite
Wikipedia : Distributivgesetz
Wikipedia : Assoziativgesetz
1.1 Terme mit mehreren Variablen
Definition: Term - Gleichung
• ein Term ist ein mathematischer Ausdruck ohne Gleichheitszeichen.
• eine Gleichung besitzt ein Gleichheitszeichen.
Auf beiden Seiten des Gleichheitszeichens stehen gleiche Werte entsprechend zweier äquivalenter Terme.
Beispiele für Terme mit mehreren Variablen
• Term mit $x$ und $y$ : $\boxed{x \cdot (y - 1)}$• Term mit $x$ und $y$ : $\boxed{2x2 - 3y +4}$
Beispiele für Gleichung mit mehreren Variablen
• Gleichung mit $x$ und $y$ : $\boxed{y = 2x + 7}$• Gleichung mit $x$ und $y$ : $\boxed{y = 4x^2 + 3x + 1}$
Rechenregel: Zusammenfassung von Termen
In Summen(Differenzen) können nur Summanden addiert(subtrahiert) werden, welche über Variablen mit gleichen Exponenten verfügen!Beispiel:
$\boxed{S = a + 3a = 4a}$
$\boxed{S = a + 3b = a + 3b}$ : kann nicht zusammengefasset werden!
$\boxed{S = a + 3b + 2a + 7b = 3a + 10b}$
In Produkten(Quotienten) können gleiche Variablen(Konstanten) zu Variablen mit Exponenten zusammengefasst werden!
Beispiel:
$\boxed{P = 2a^2 + 3a^2= 5a^2}$
$\boxed{P = a^2 + b^2 = a^2 + b^2}$ : kann nicht zusammengefasset werden!
$\boxed{P = x^2 + 2y^2 + x^2 + 2y^2 = 2x^2 + 4y^2}$
Beispiel: Zusammenfassung von Summanden
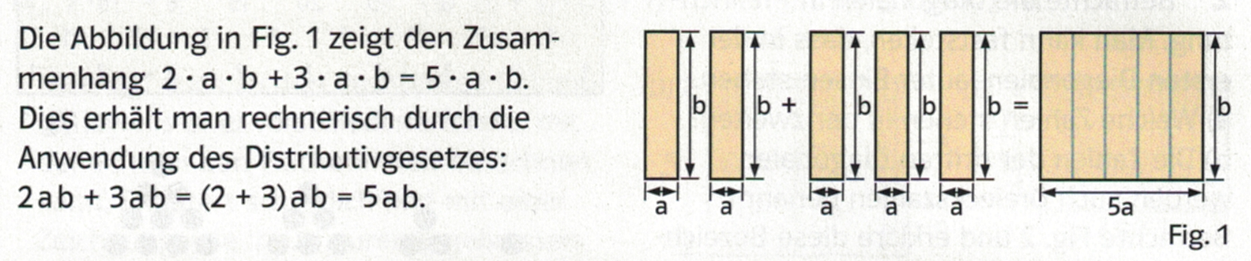
Beispiel: Flächenberechnung

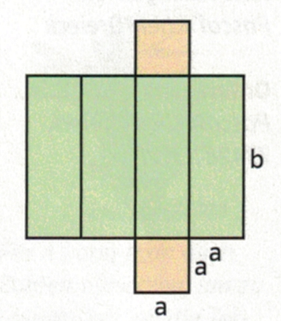
Das Volumen $V_Q$ eines Quaders berechnet sich zu: $~~~\boxed{V_Q = a^2b}$
Aufgabe: Fasse den Term soweit wie möglich zusammen:
$\boxed{T = 5x \cdot 2y \cdot x^2 \cdot 4 - (5y \cdot 4 - 2x^3y)}$
$T = 5 \cdot 2 \cdot 4 \cdot x^3 \cdot y - 5y \cdot 4 + 2x^3y$
$T = 40x^3 y - 20y + 2x^3y$
$\boxed{T = 42x^3 y - 20y}$
Aufgabe: Löse die Klammern auf und fasse soweit wie möglich zusammen:
$\boxed{T = \dfrac{1}{2}p + (\dfrac{2}{3}q - \dfrac{p}{2} + q)}$
$T = \dfrac{1}{2}p + [(\dfrac{2}{3} + \dfrac{1}{1})q - \dfrac{p}{2}]$
$T = \dfrac{1}{2}p + [\dfrac{5}{3}q - \dfrac{p}{2}]$
$T = \dfrac{1}{2}p - \dfrac{p}{2} + \dfrac{5}{3}q$
$\boxed{T = \dfrac{5}{3}q}$
Aufgabe: Fasse soweit wie möglich zusammen:
$\boxed{T = 3a \cdot 2b + 4ab}$
$T = 3 \cdot 2 \cdot ab + 4ab$
$T = 6ab + 4ab$
$\boxed{T = 10ab}$
Homepage WebSites Unterrichtsstunden Mathematik